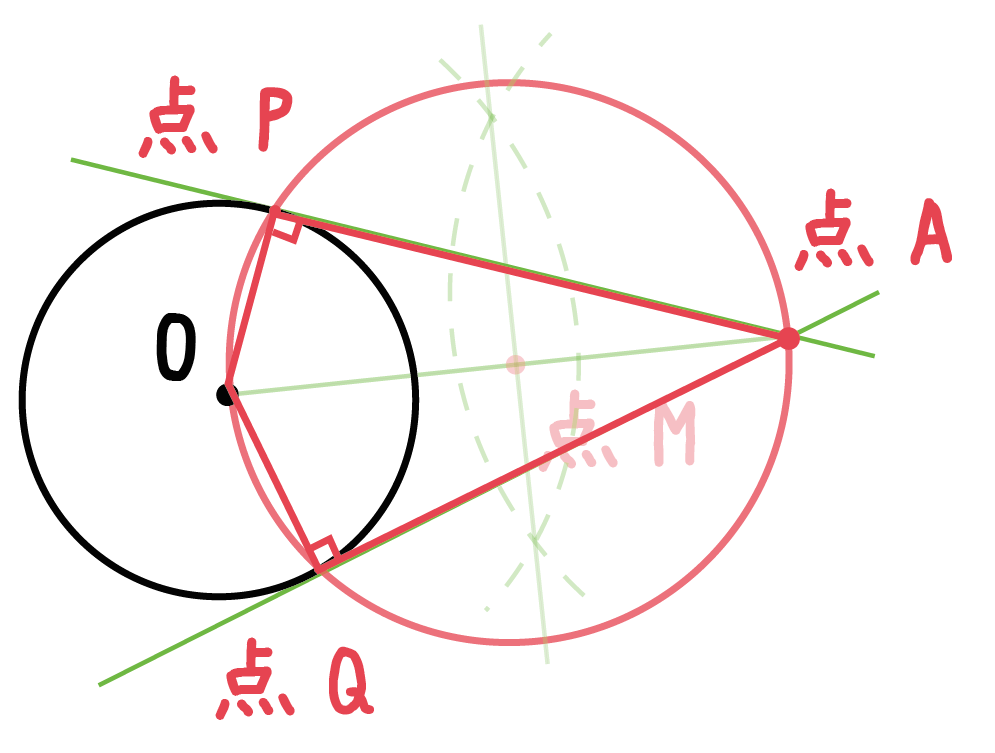
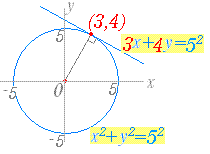
円の外部の点から円に引いた接線は、2つ引くことができます。 そのため、接点は2つできます。 これを $\mathrm{ P }(p_1,p_2)$, $\mathrm{ Q }(q_1,q_2)$ とおくことにしましょう。接点の座標をP(x 1 ,y 1) とおくと、接線の方程式はx 1 x y 1 y = 5 ・・・① これが(‐3,‐1)を通るので3x 1 y 1 = 5 ・・・② また点Pは円x 2 y 2 = 5上の点なので x 1 2 y 1 2 = 5 ・・・③ ②よりy 1 = 3x 1 5 ・・・④ ④を③に代入すると x 1 2 (3x 1 5) 2 = 5 展開して整理すると大小2つの円 p, q が交わっている。 図2-1 2本の共通接線がr で交わっていて e , g は円p での接点としf, g は円q での接点とする。 r を通る直線をひき円p との交点をa, c とし 円q との交点をb, d とする。 この状況で成り立つことを幾つか述べていこう。 3
円と直線の接点の座標の求め方について教えてください 円 x 2 Yahoo 知恵袋
円 接点 角度
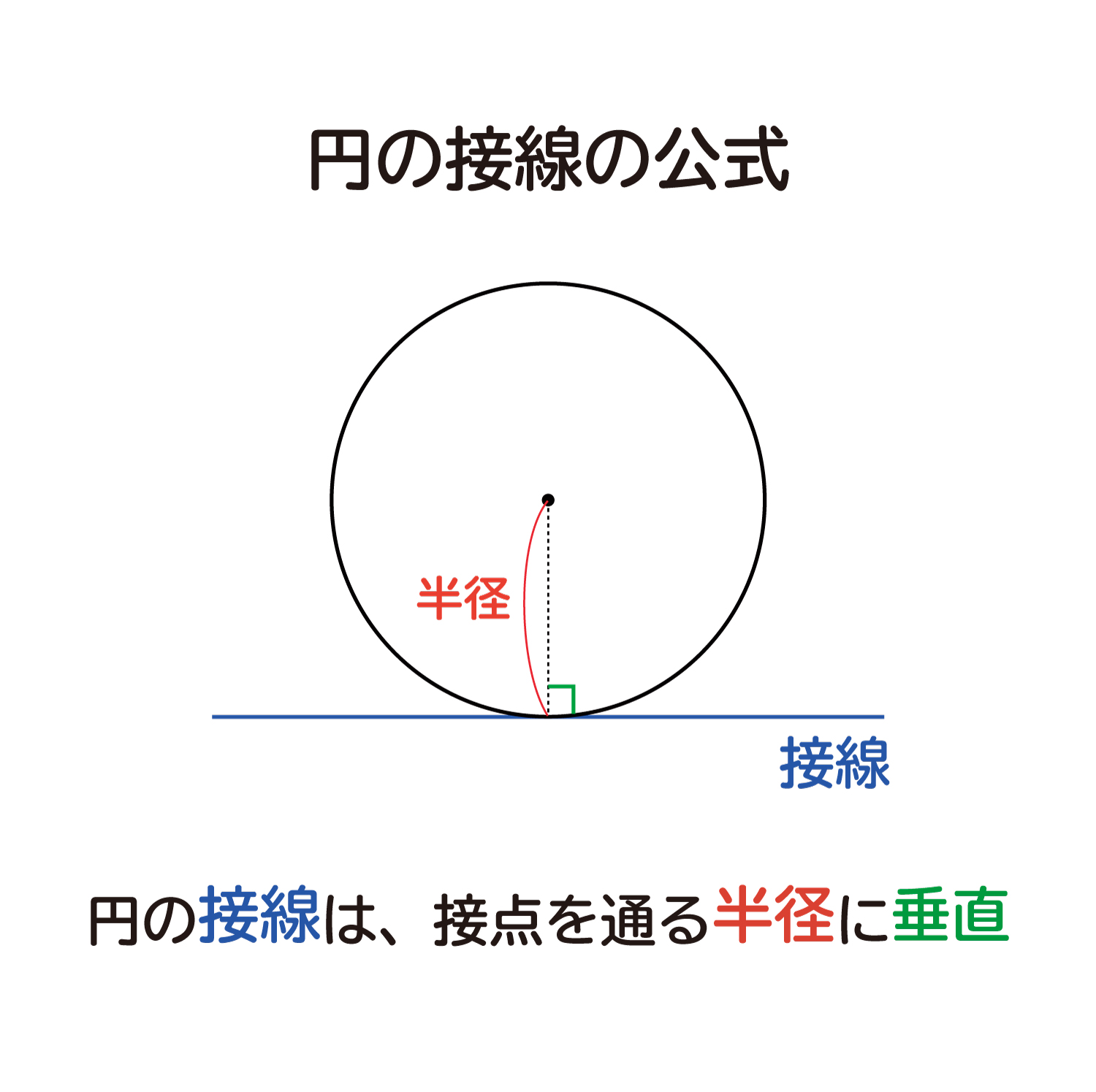
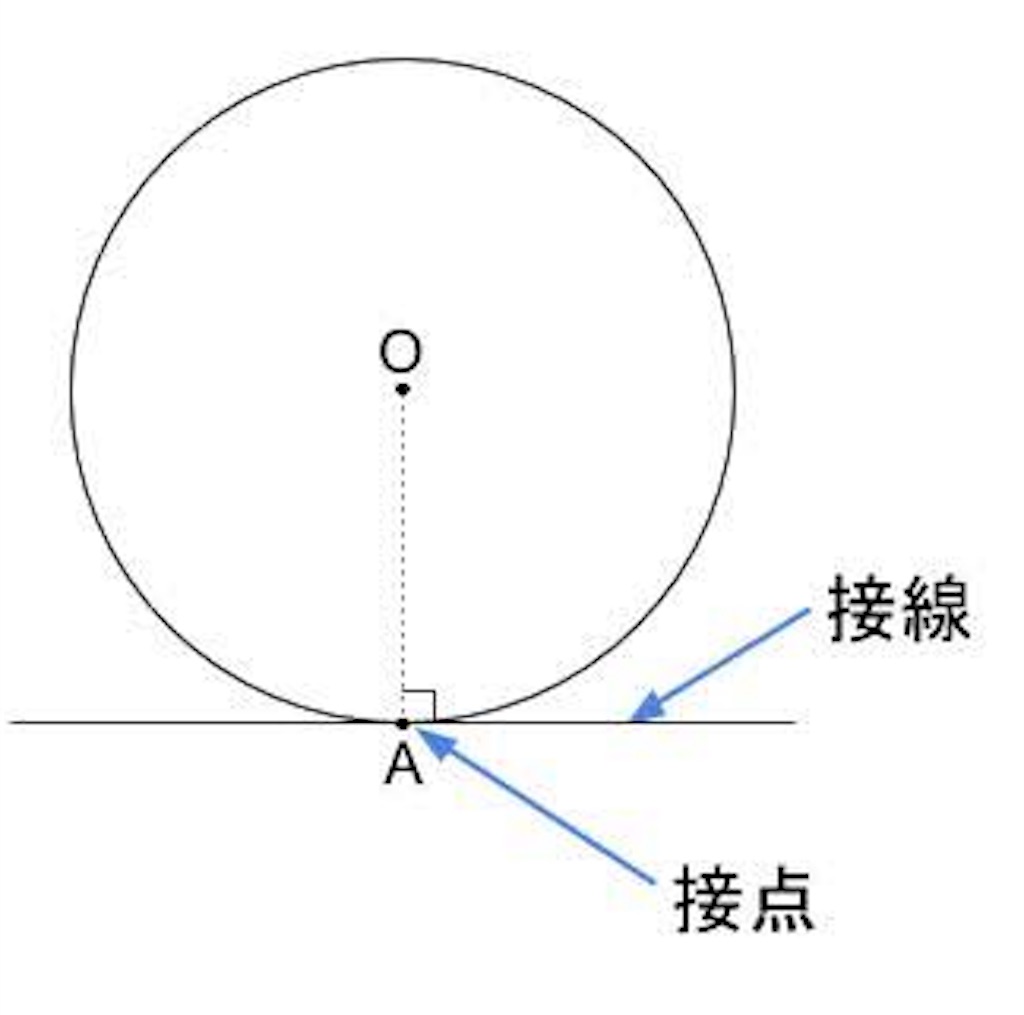
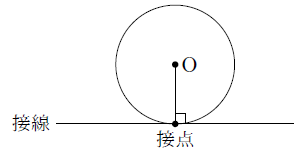
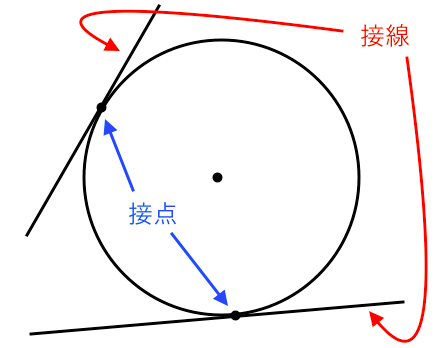
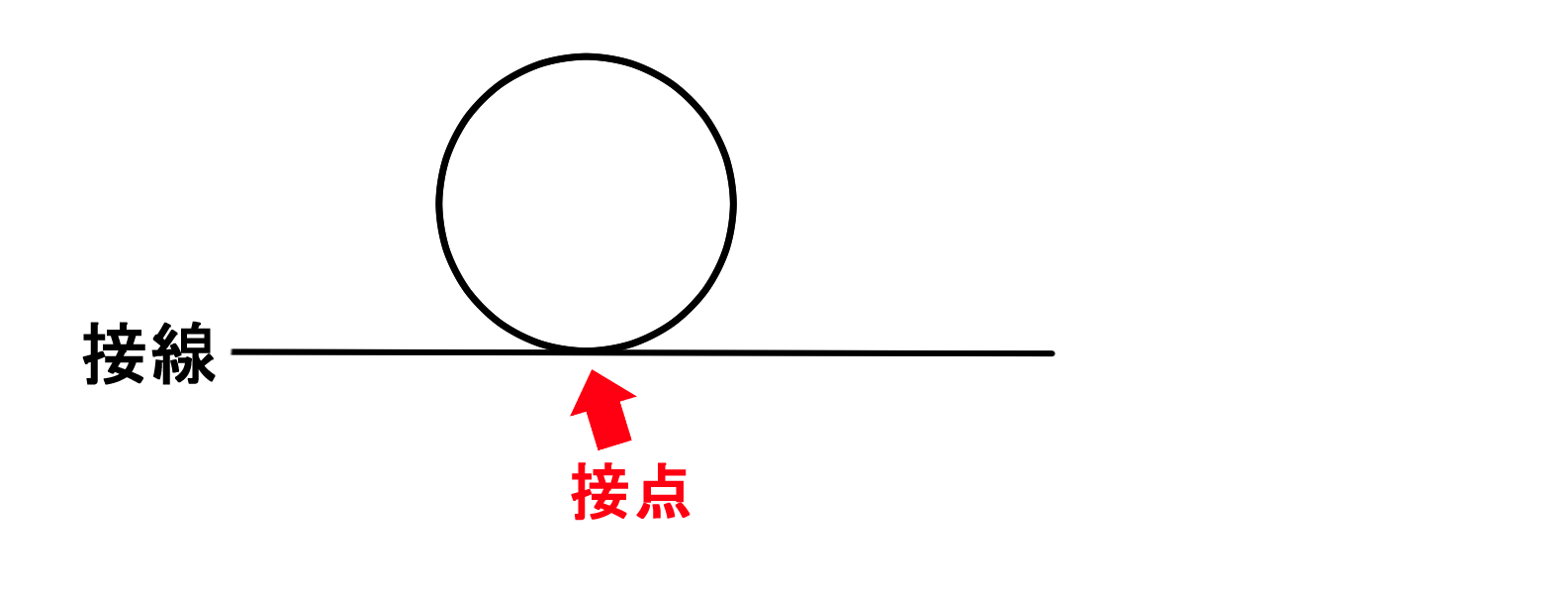
円 接点 角度-円を作成します。 検索 次のプロンプトが表示されます。 中心点 中心点と、直径または半径の値に基づいて円を作成します。 半径 値を入力するか、点を指定します。 例 直径(D) 値を入力するか、2 点目を指定します。 例 3 点(3P) 円周上の 3 点に基づいて円を作成します。 例 接点、接点 円と直線が接するということは このように 「円の中心と接点を結んだ線分」 と 「接線」 は 必ず垂直 になります。




点から円への接点を求める Qiita
ただし, D, E, F D,E,F D, E, F は内接円と各辺の接点, S S S は A B C ABC A BC の面積, r r r は内接円の半径, s = a b c 2 s=\dfrac{abc}{2} s = 2 a b c です。 以下ではこの2つの性質を傍心に応用するとどうなるか考えてみます。点 a を通る円との接線を2本引き、その接点を点 b、点 c とします。2つの接点と点 o を結ぶ線を引くと四角形 obac ができます。この四角形の対角線 oa を引いたとき、∠aoc(θ1)を求めます。 今回は θ の角度がわかっている場合を考えます。円1の半径 R= 25 , 中心(xc1,yc1) = ( 05, 2) とする。 円2の半径 R= 15 , 中心(xc2,yc2) = ( 3, 7) とする。 、 エクセルを用い円1と円2の共通接線を求めてみよう。 図3 円と円の共通接線とそのグラフ うまく接線が求まりました。
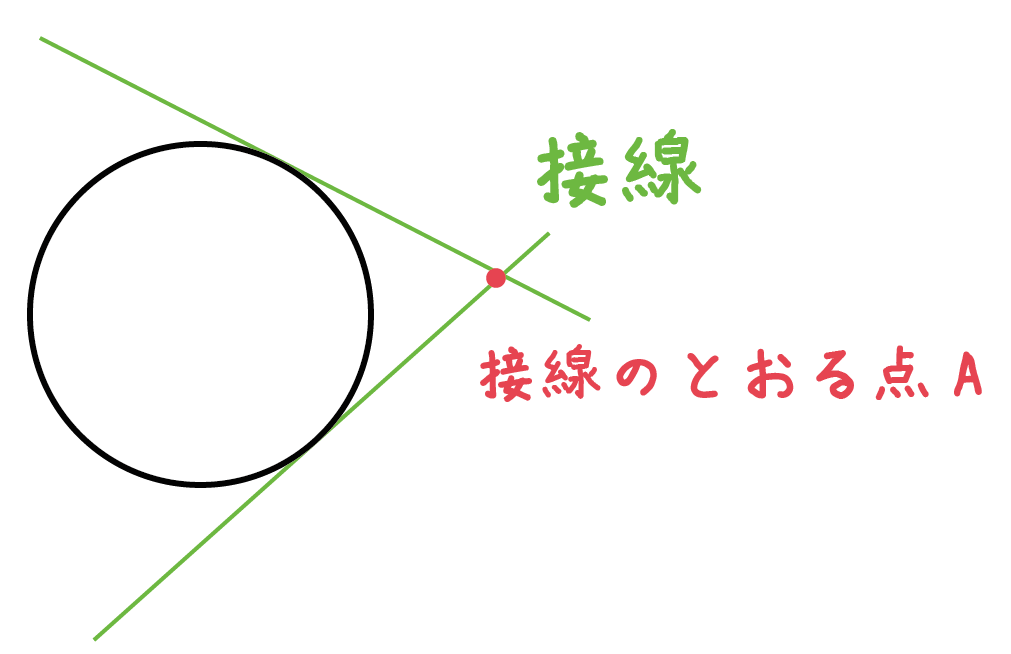
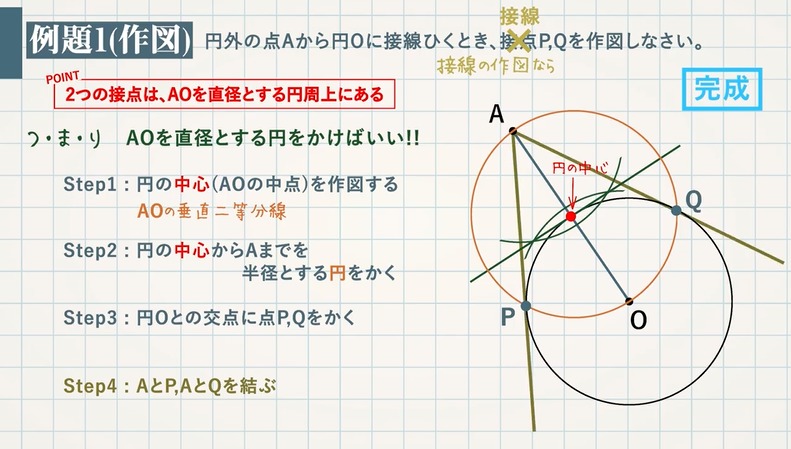
円に接す線を 接線 、接する点を 接点 といいます。 POINT:接線は、接点を通る半径に垂直 図の $\rm AO$ を結ぶと $2$ つのことがわかります。 「 円周角の定理の逆 」から POINT: $\textcolor{blue}{2}$ つの接点は、 $\textcolor{blue}{\rm AO}$ を直径とする円周上にある。 直角三角形の合同条件「 斜辺と他 点(4, 6)を通り、円 (x -1)2 (y - 1)2 = 9 に接する直線の方程式は? 今回の円は、中心 (1, 1)なので、原点中心にするために、 x方向に-1, y方向に-1 だけ平行移動させます。 与えられた点 (4, 6)も同様に平行移動させます。 原点を中心とする円の接線の方程式 円 x2 y2 = r2 x 2 y 2 = r 2 に接する直線、つまり、接線の方程式について考えましょう。 接線は何本でも引けますが、接点を決めれば接線は1本に決まります。 ここでは、接点を (x1,y1) (x 1, y 1) としましょう。
Jw_cadの作図(2)の〔 接線 〕は図面作成画面内描かれた円と円を繋ぐときや点と円を繋ぐときに使うコマンドですが、「円上点指定」を使えば線が円に接する点を指定することができます。 〔接線〕円上点指定の使い方 〔 接線 〕コマンドを実行し、コントロールバーの「円上点指定」の「8 – 円2 – 接点・接点・半径で円を描く」へ最初のコメントを投稿しませんか? vip会員ならコメントを投稿できます! vip会員について詳しく知る ログインしてコメントを書く このときの交点を円と直線の 接点 、直線を円の 接線 という。 中心の座標が $ (x_0,y_0)$ 半径 $r$ の円と、直線 $axbyc=0$ の位置関係が1点で接するとして、その接点 $H$ の座標を求める。 点 $H$ の座標は、点 $C$ の位置ベクトルを $\vec {c}$ とすると、



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル
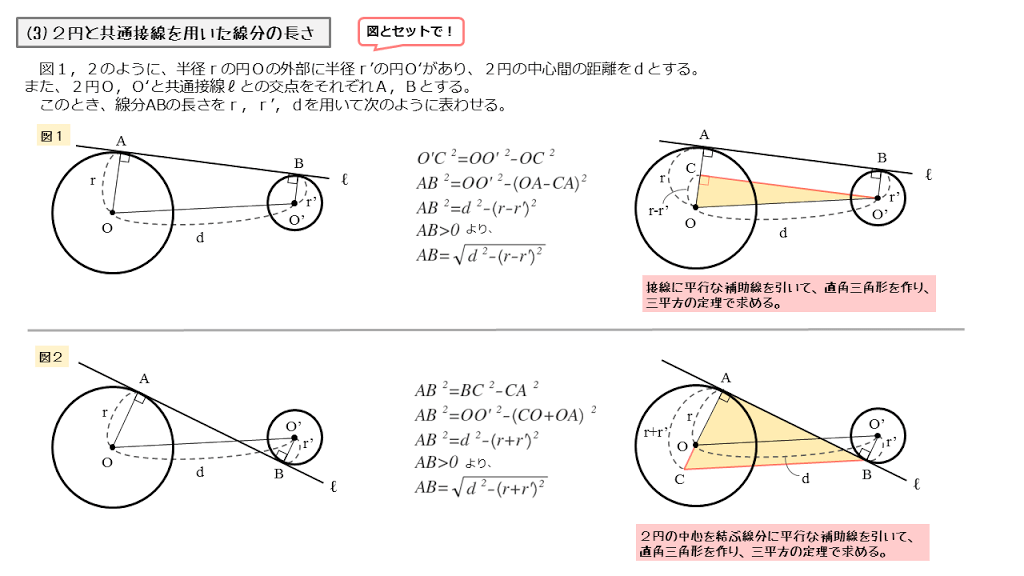



図形の性質 2円の位置関係について 日々是鍛錬 ひびこれたんれん
円と円の交点を求めてみます。 どちらの円も任意の位置にあると面倒なので、片方の円は原点中心とします。 上の円の方程式から、下の円の方程式を引きます。 ここで、 とおけば、 と直線の方程式と∴ 円の外部の点pから引いた接線の接点をt、pを通り円と2点で交わる直線との交点をa, bとする ⇔ ( ならば ) pt 2 = pb・pa // 《 例 》 図のようなとき、x, y を求めましょう → 相似な2つを見つけるだけ 「円の接線 A T と弦 A B が作る角 ∠ B A T は、弦 A B に対する円周角 ∠ A C B と等しい」という定理を、 接弦定理 と言います。 接弦定理は、 ∠ B A T が鋭角・直角・鈍角のどの場合でも成り立ちますが、それぞれ証明の仕方が少しずつ変わってきます。




点から円への接点を求める Qiita



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル
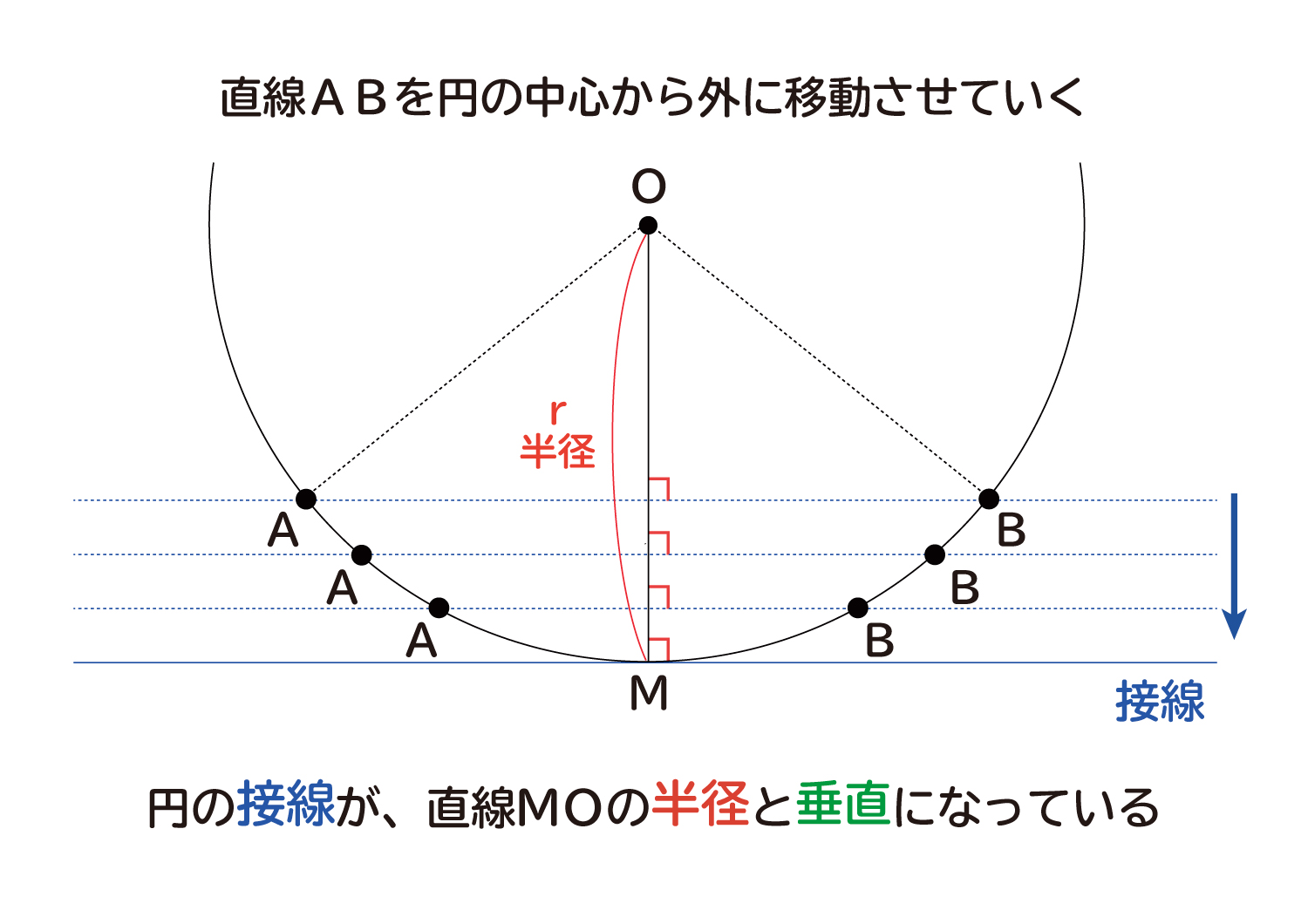
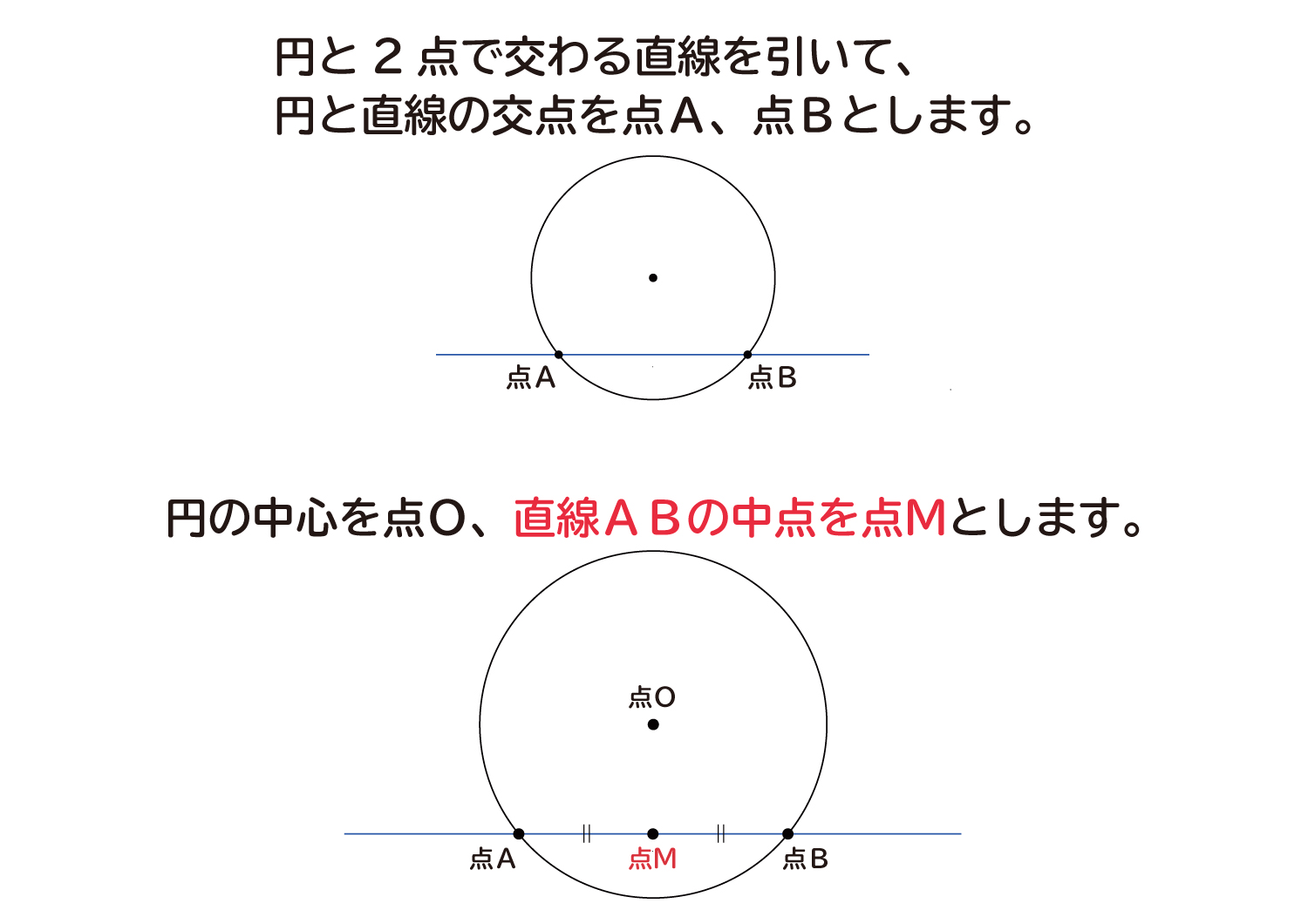
交点・接点計算 接円計算 円の中心計算 ・直線と直線の交点 ・直線と円の交点 ・円と円の交点 ・極座標 ・点の回転2円の交点を通る円の方程式 → 携帯版は別頁 円と接線の方程式 円周上の接点の座標が与えられたとき,その点に「 おける 」接線の方程式は次の公式で求めることができる(前出). 円 x2y2=r2 の周上の点 (p , q) における接線の方程式は pxqy=r2「円の接線は、接点を通る半径に垂直」になる説明 まずは、下の図のように 円と2点で交わる直線を引いて 、円と直線の 交点を点A、点B とします。 円の中心を点O 、 直線ABの中点を点M とします。



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




点から円への接点を求める Qiita
概要 円1 中心\((x_1, y_1)\) 半径\(r_1\) と 円2 中心\((x_2, y_2)\) 半径\(r_2\) の2つの円がなす共通接線の接点を求める。 (円1の方の)共通内接接点がわからない時の、接線の求め方が知りたいです =>作者: 連絡ありがとう.サブメニューでその次の項目を見てください. 個別の頁からの質問に対する回答 円の接線の方程式 につい図2の接点S1と円の逆側にある接点S2の座標を求める。 P点から円の中心までの距離(L)は L = √( ( xcxp) 2 ( ycyp) 2) となる。 P点から円の中心への角度(α)は




円外の点から引いた接線 おいしい数学




円の接線の方程式
たまに 円外の点 (p,q)に関する 円の接線の式をpxqy=r 2 と 勘違い する人がいますが,この式は 接線でなく極線の方程式 なのです。 円の接線の方程式 円 x2 y2 = r2 の円周上の1点 P(x0, y0)




2 P Q X2y25 P Descubre Como Resolverlo En Qanda



Autocad Lt はじめての作図 Autocad Lt 円作図



Math 三角形に内接する円 働きアリ




勉強しよう数学 ベクトルで円の二接線の交点 極 を求める 解の変換
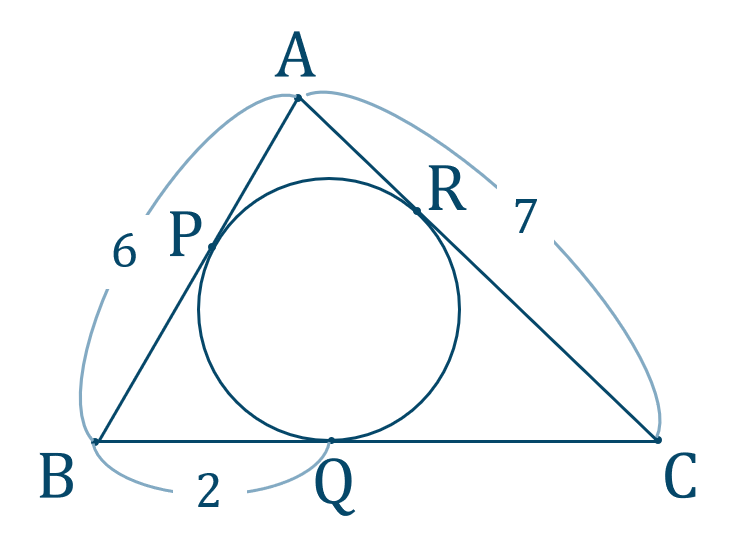



数学a 内接円と接線の条件の使い方とコツ 教科書より詳しい高校数学
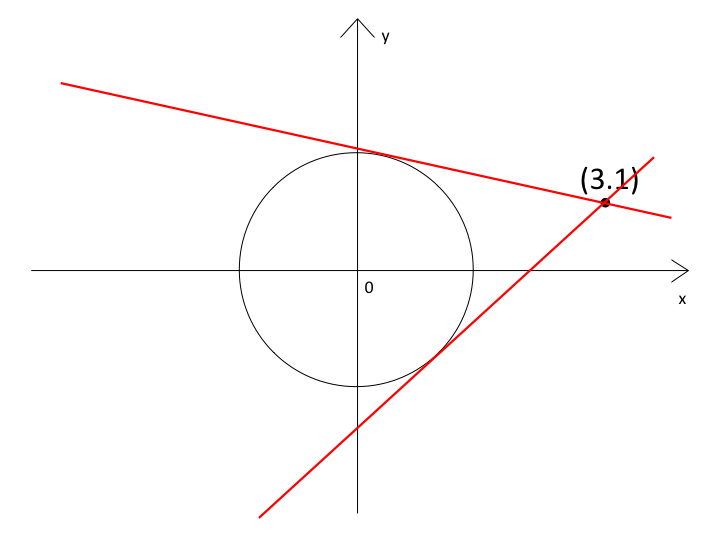



3分で分かる 円の接線を求める公式とその使い方をわかりやすく 合格サプリ




勉強しよう数学 点aを通る直線の円への接点をベクトルの内積を利用して解く




Atは円oの接線 Aは接点の時の角8を求める問題です 答えは 8 Clear



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル
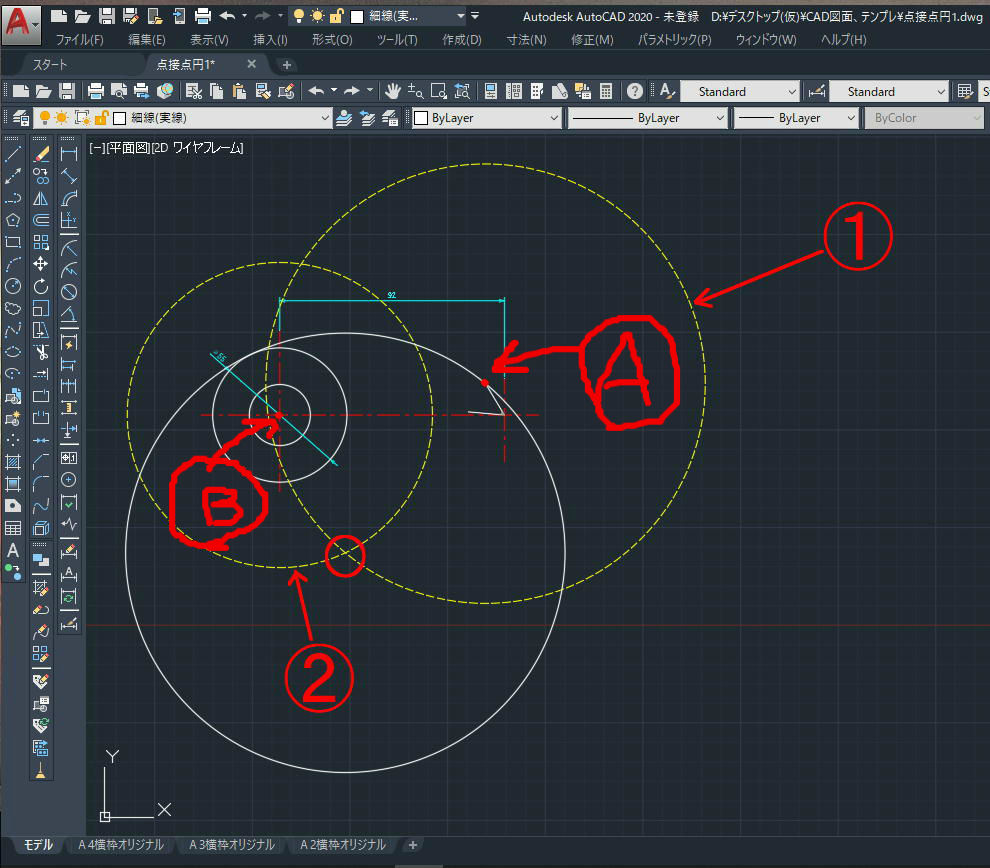



Auto Cad 円作成機能に 接点 交点 半径 は無いの メカ モスラ mechamothra のメカ日記



1




勉強しよう数学 円の極の座標の解の変換



1
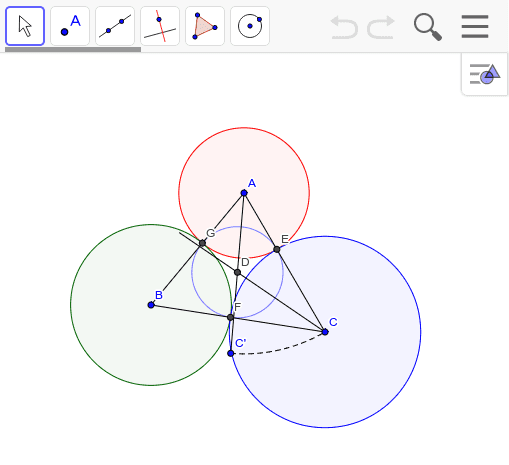



2円に接する円の作図 Geogebra




応用 2つの接点を通る直線 なかけんの数学ノート



点から円への接点を求める Qiita




円の2つの接点を通る直線 極線 の解説 Youtube



円の接線と角度 中学から数学だいすき



1




高校数学a 2つの円の共通外接線と共通内接線の長さ 受験の月
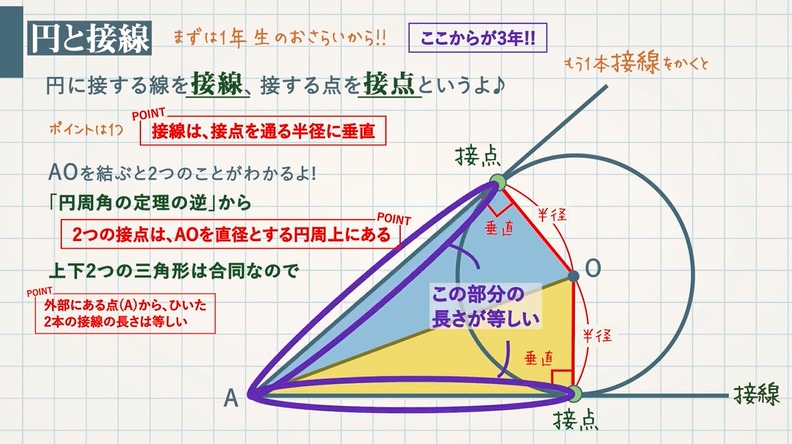



円と接線 教遊者



頂点と接点を結ぶと
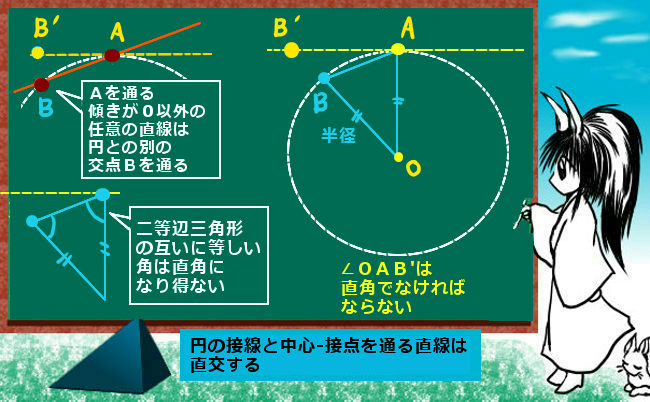



円の接線と内接 外接 理数系無料オンライン学習 Kori



知ってると得 円の接線の作図 円に接する円の作図方法 はてなラボ




高校数学 円と放物線の位置関係 受験の月
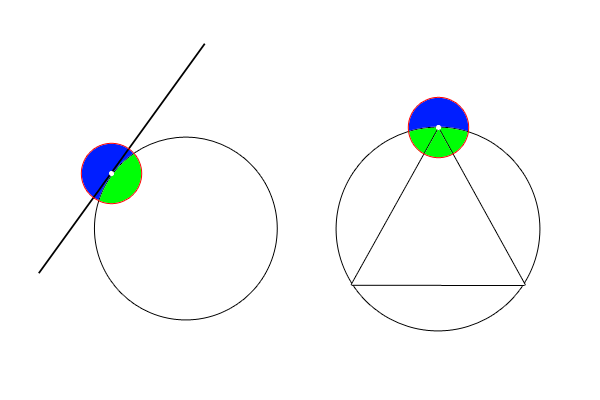



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター




山と数学 そして英語 高校数 図形と方程式 円の方程式 放物線と円の接点 共有点
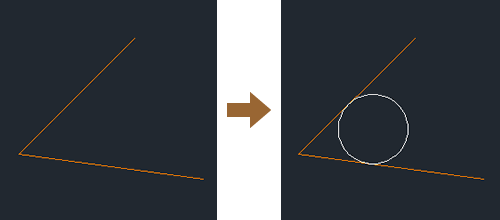



8 円2 接点 接点 半径で円を描く Autocad 使い方徹底ナビ
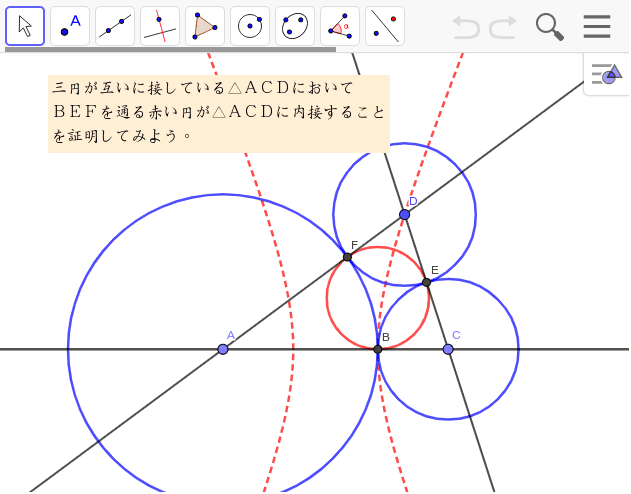



接点の作る円は内接円 Geogebra




勉強しよう数学 複素数計算で円外の点からの直線の円への接点を求める




接線と円の関係 Jsciencer



円の接線の長さ まなびの学園



円の接線の方程式



点から円への接点を求める Qiita



円と直線の接点の座標の求め方について教えてください 円 x 2 Yahoo 知恵袋



Nutsu As 円と円の接線



円の作図と円の接線の作図 チーム エン



Math Battle 0250 半円の共通接線と接点間距離
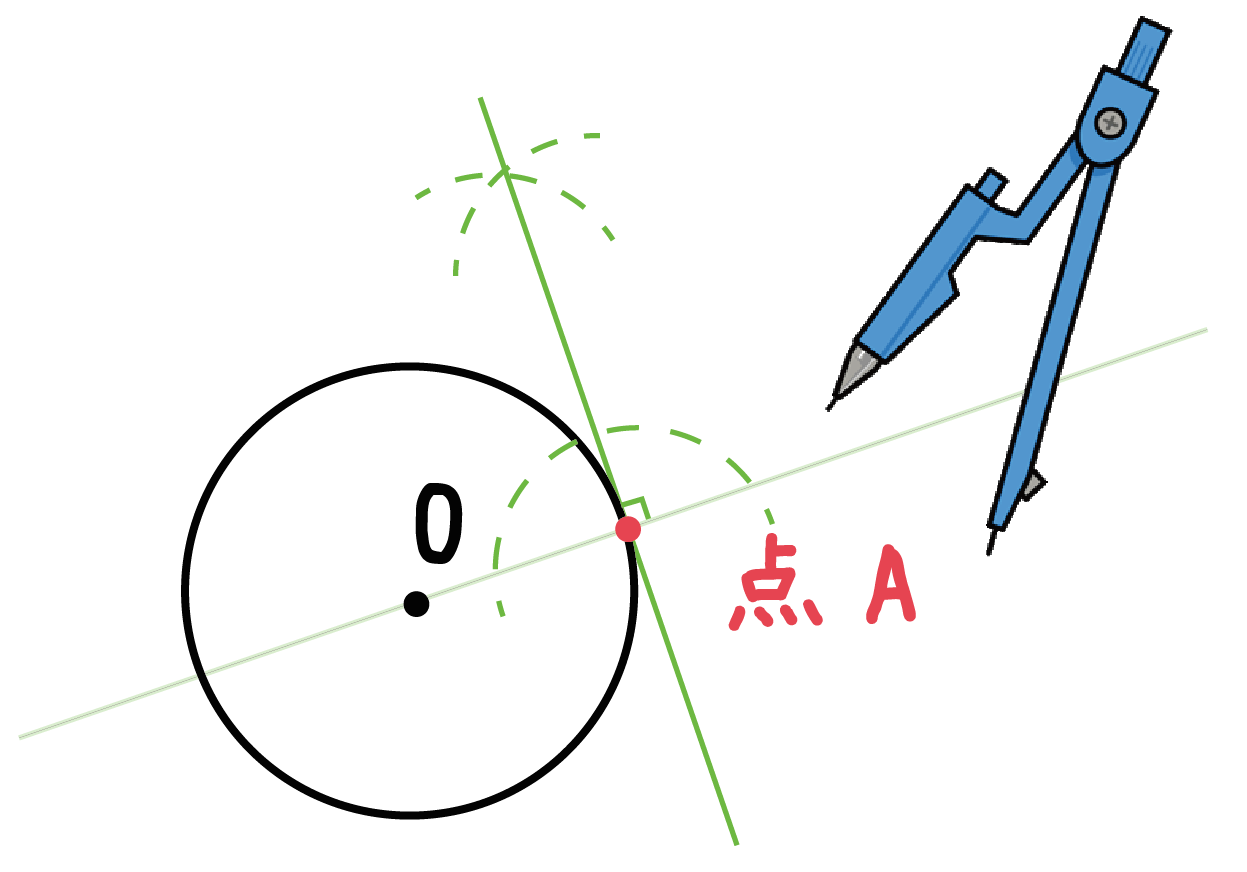



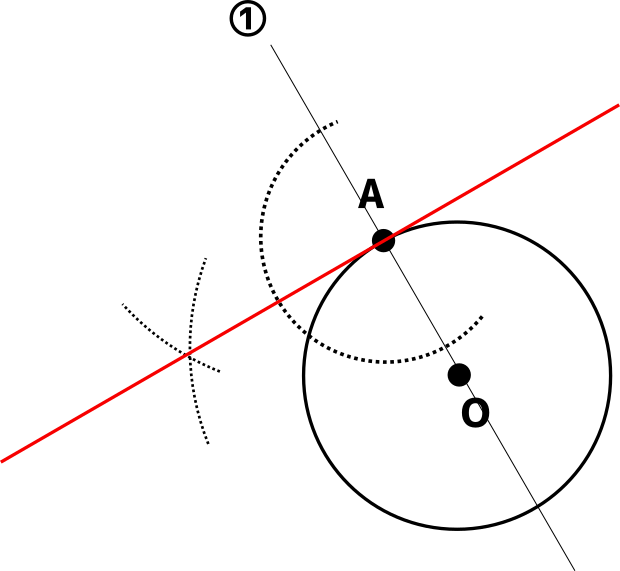
中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




円の極と極線 円外の点から引いた2つの接線の接点を通る直線 数学の偏差値を上げて合格を目指す




高校数学 円に関する極と極線 受験の月
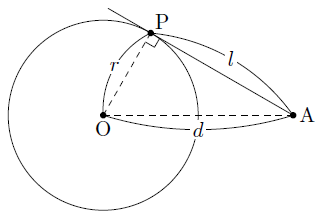



円の接線の長さ まなびの学園




点から円への接点を求める Qiita




接点 伊東市の家庭教師
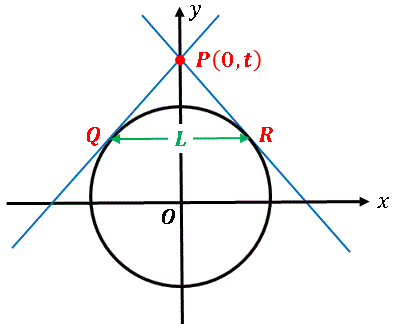



2接点の間の距離を求めます
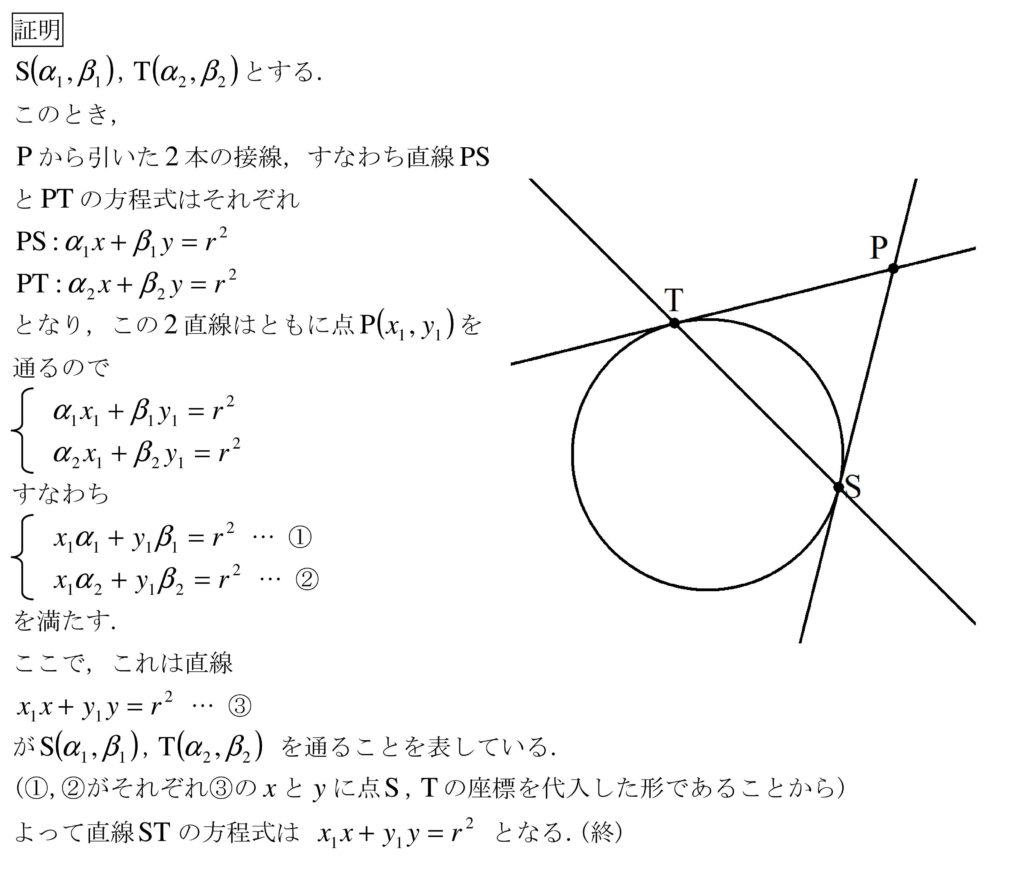



円の2接点を通る直線の公式 白銀の茶室




外接三角形が一点で交わることの証明 Geogebra
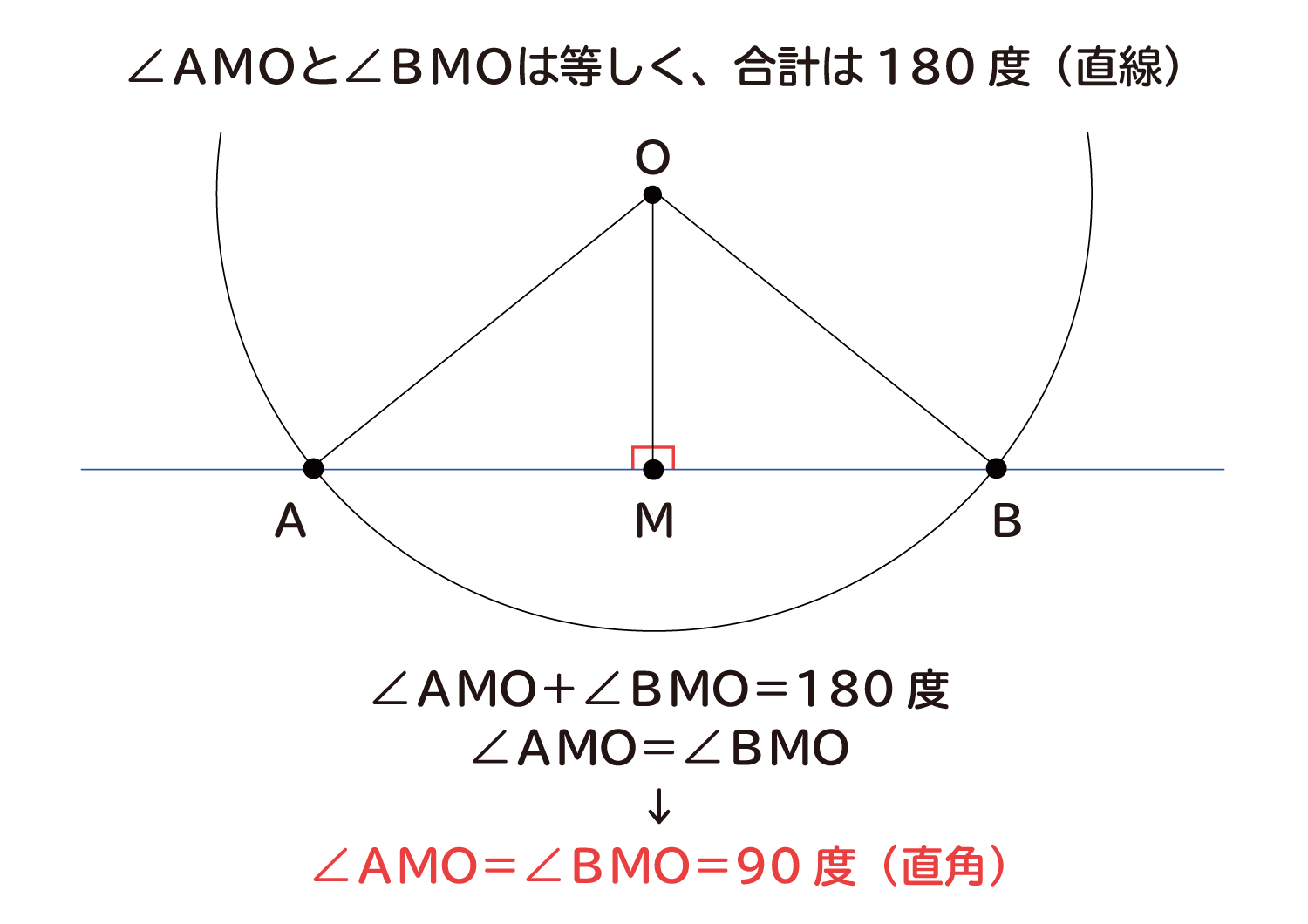



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




勉強しよう数学3c 楕円と円の接点




接線の性質 なぜこの記号同士が同じ角度になるのかが分かりません Clear




円の接線の方程式を求める公式と証明 高校数学の知識庫



円と接線 教遊者




勉強しよう数学 点aを通る直線の円への接点は図形で求めること



接線と接点について知ろう 苦手な数学を簡単に



点から円への接点を求める Qiita




1 X2y22x4y 40 2 Descubre Como Resolverlo En Qanda



円の作図と円の接線の作図 チーム エン
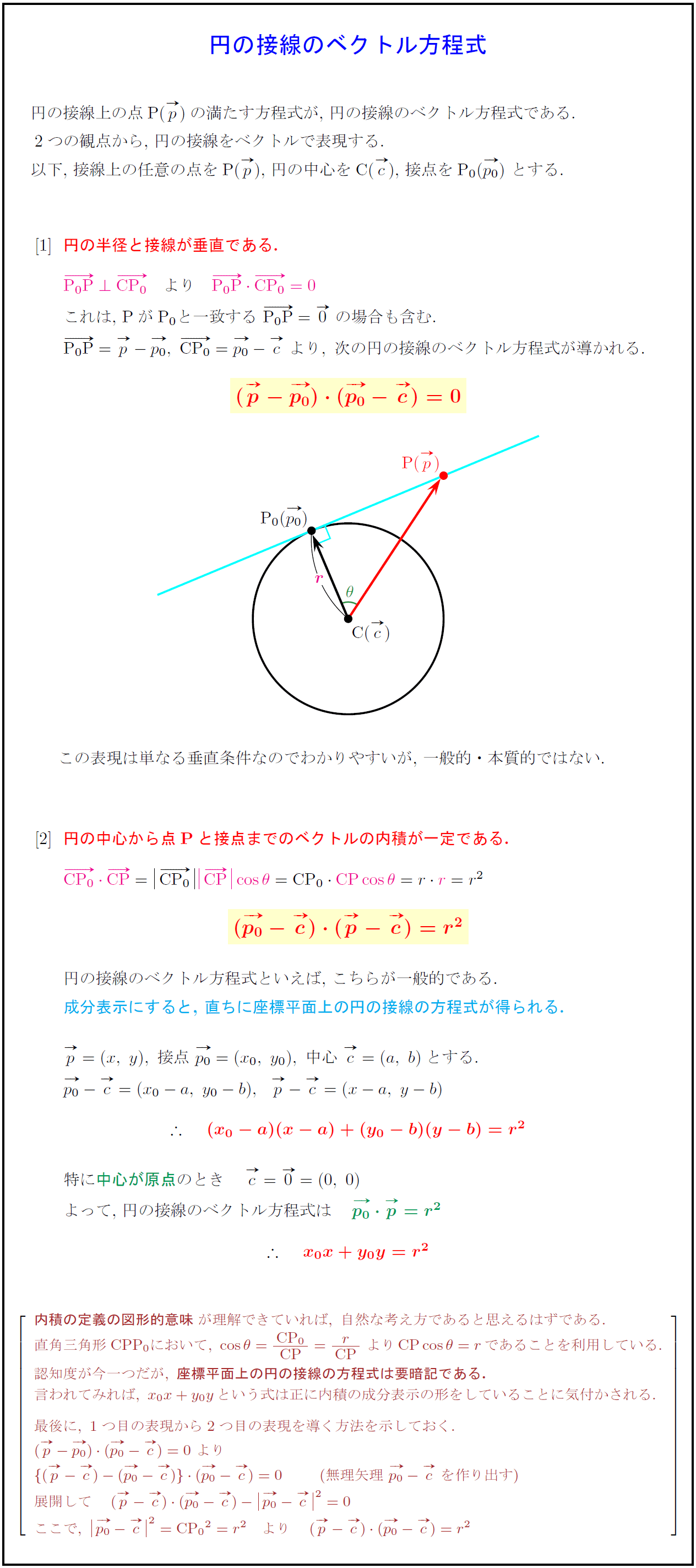



高校数学b 円の接線のベクトル方程式2パターン 受験の月



円と接線




円の接線の295 298の解説をお願いします Clear



48s96ub7b0z5f Net Futatsu En Sessen
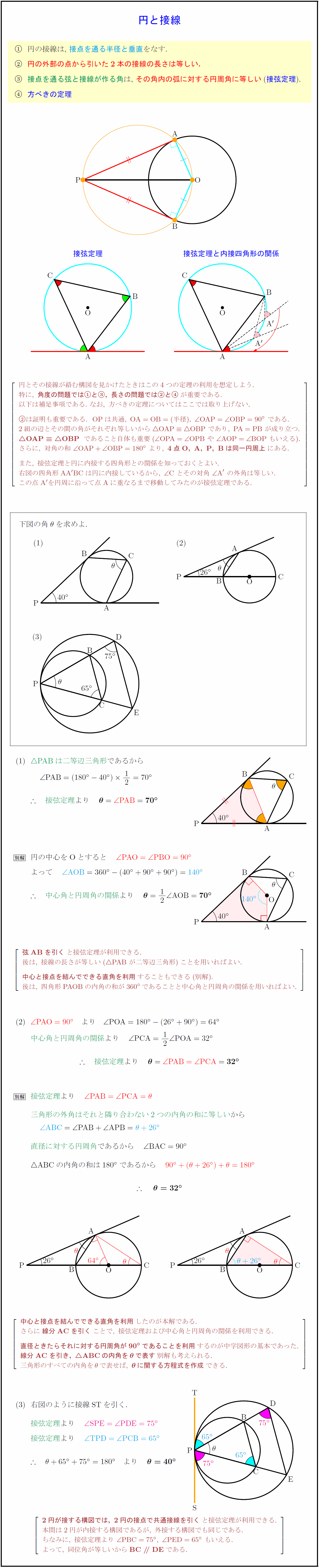



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月
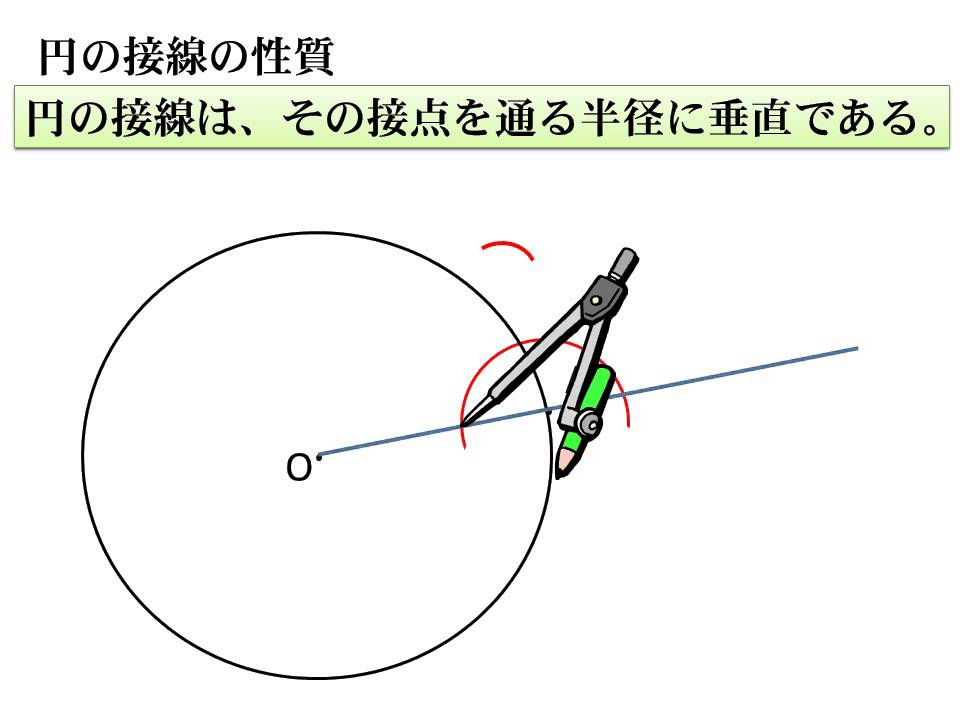



中学校数学1年 円の接線の作図 Youtube



円と直線の関係




なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




点a A B を通り円x Y R に接する直線の方程式の求め方 数学ii By ふぇるまー マナペディア




高校数学 円の外部の点から引いた円の接線 映像授業のtry It トライイット




1 Po A Pa Pb Q R Pa31 Descubre Como Resolverlo En Qanda




円の極と極線 島根大 大学入試数学の考え方と解法
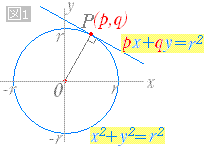



円の接線の方程式
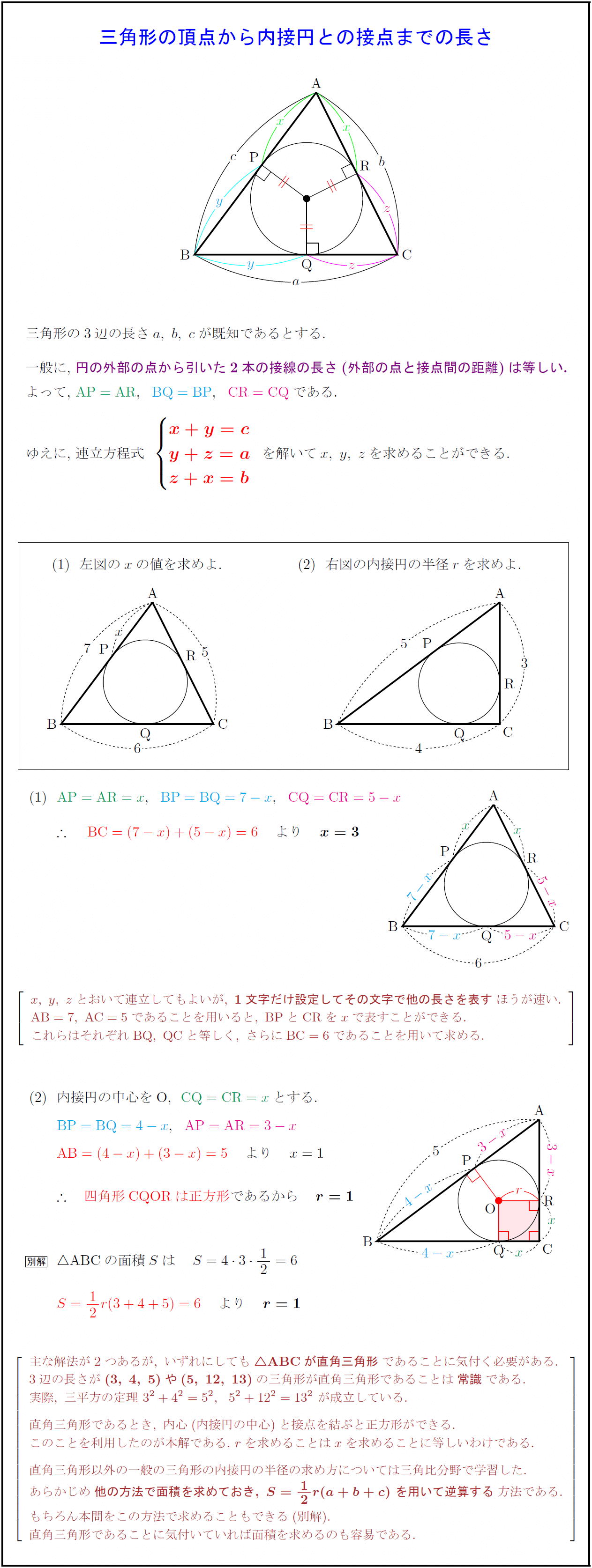



高校数学a 三角形の頂点から内接円との接点までの長さ 受験の月
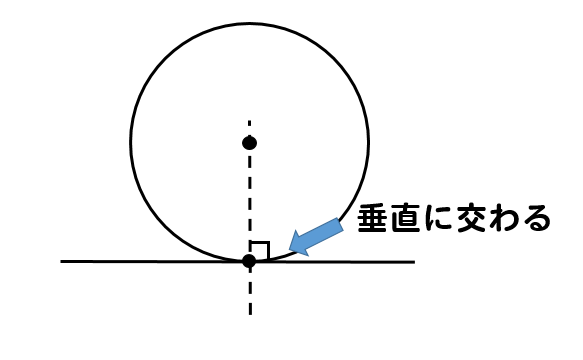



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ




195の接点の座標の求め方が分かりません なぜ接点のx座標は の重解なのですか また Clear
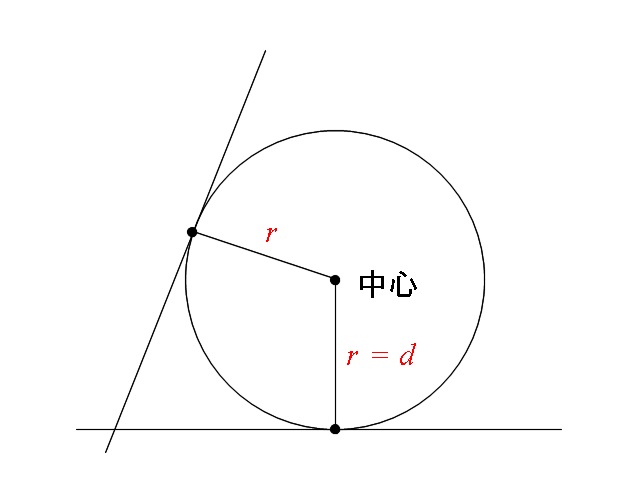



円に接する直線 接線の方程式 の求め方3パターン



数学で質問です 円の2接点を通る直線と円の接線の方程式の式は何 Yahoo 知恵袋



円外の点から引いた接線と その円との接点の中点が円の中心と円 Yahoo 知恵袋




円の接線の295 298の解説をお願いします Clear




座標上の2つの円の位置関係 数学ii By ふぇるまー マナペディア



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学
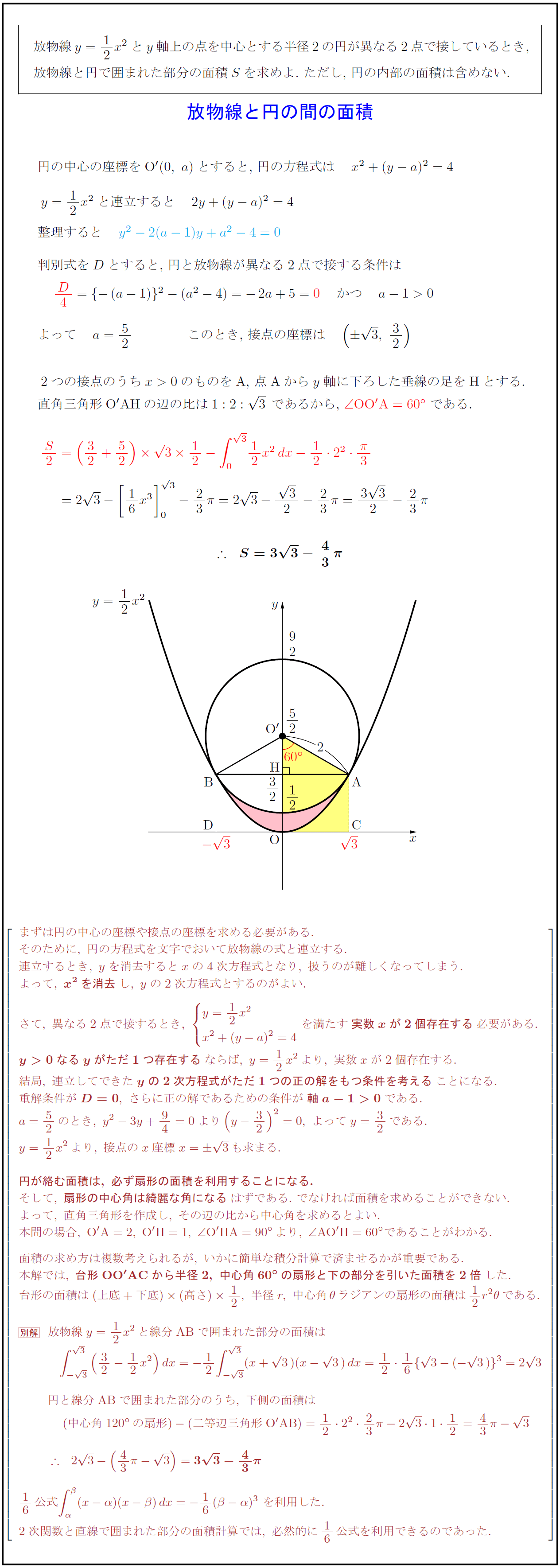



高校数学 放物線と円の間の面積 受験の月



1




2 P Q X2y25 P Descubre Como Resolverlo En Qanda
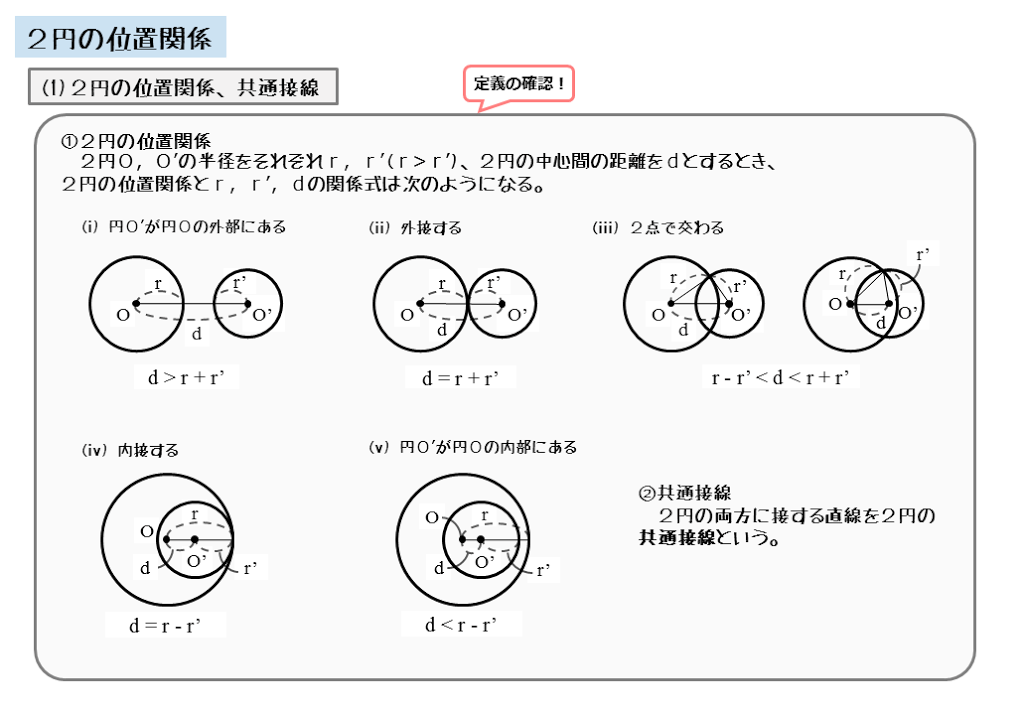



図形の性質 2円の位置関係について 日々是鍛錬 ひびこれたんれん




高校数学 円の接線公式 映像授業のtry It トライイット




数学 円の接線の方程式の求め方 解法 接点を求めて計算量を軽くしたい 高校 数学 図形と方程式 数学2 質問ありがとうございます 行間 ぎょうのあいだ 先生
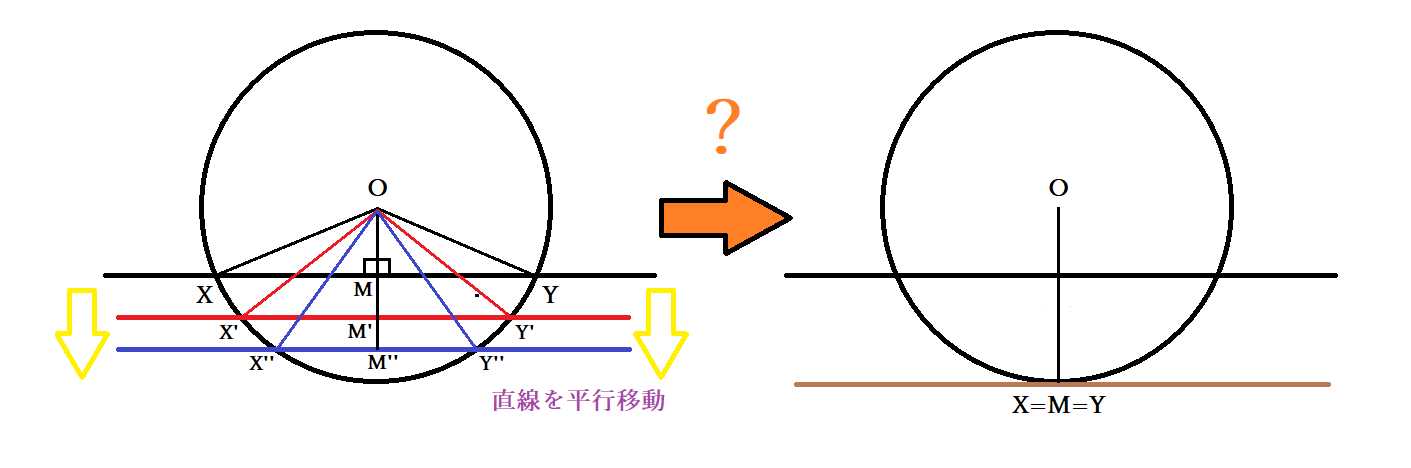



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog




基本 円の接線の方程式 なかけんの数学ノート
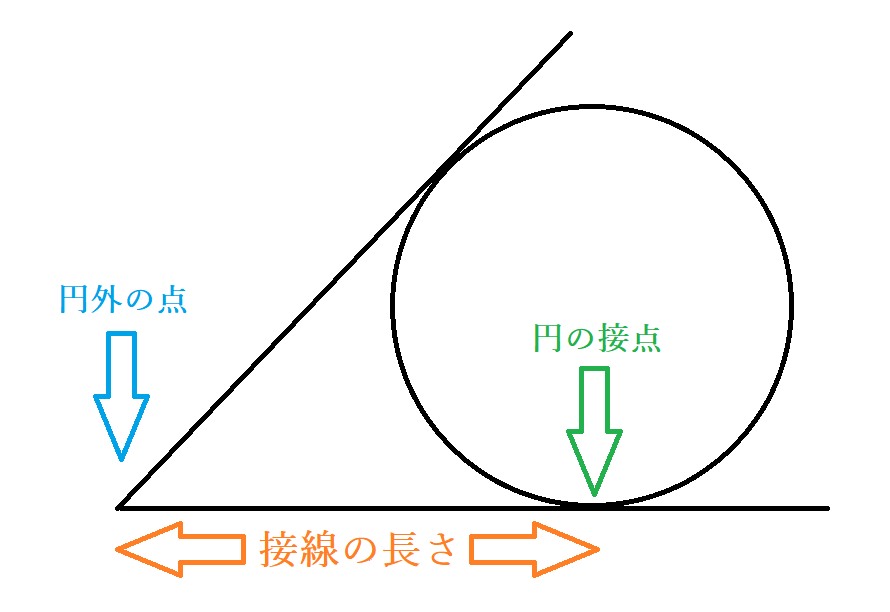



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog
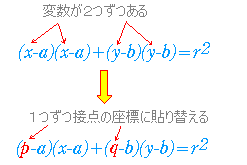



円の接線の方程式




標準 円の接線と作図 なかけんの数学ノート
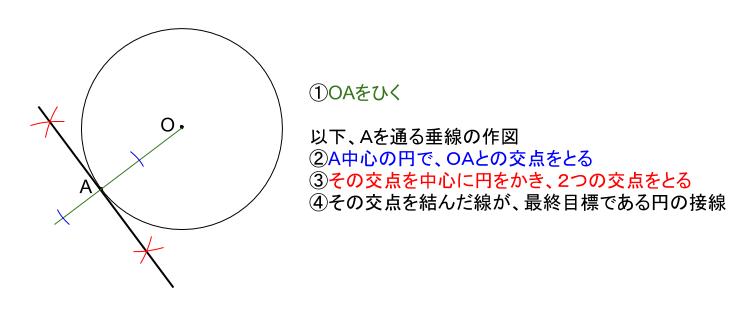



中学数学 作図 円と接線 接点 中学数学の無料オンライン学習サイトchu Su
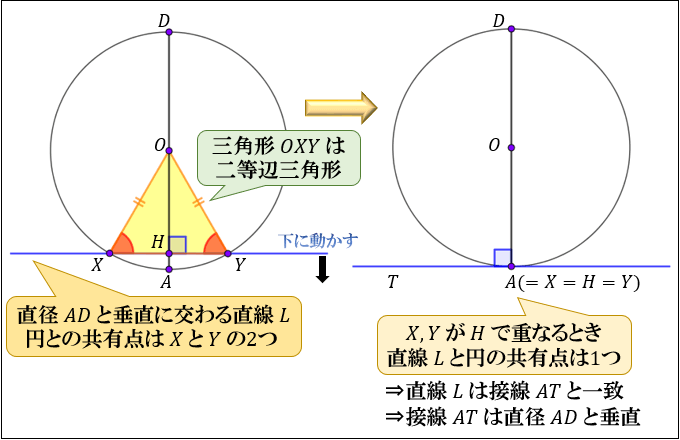



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
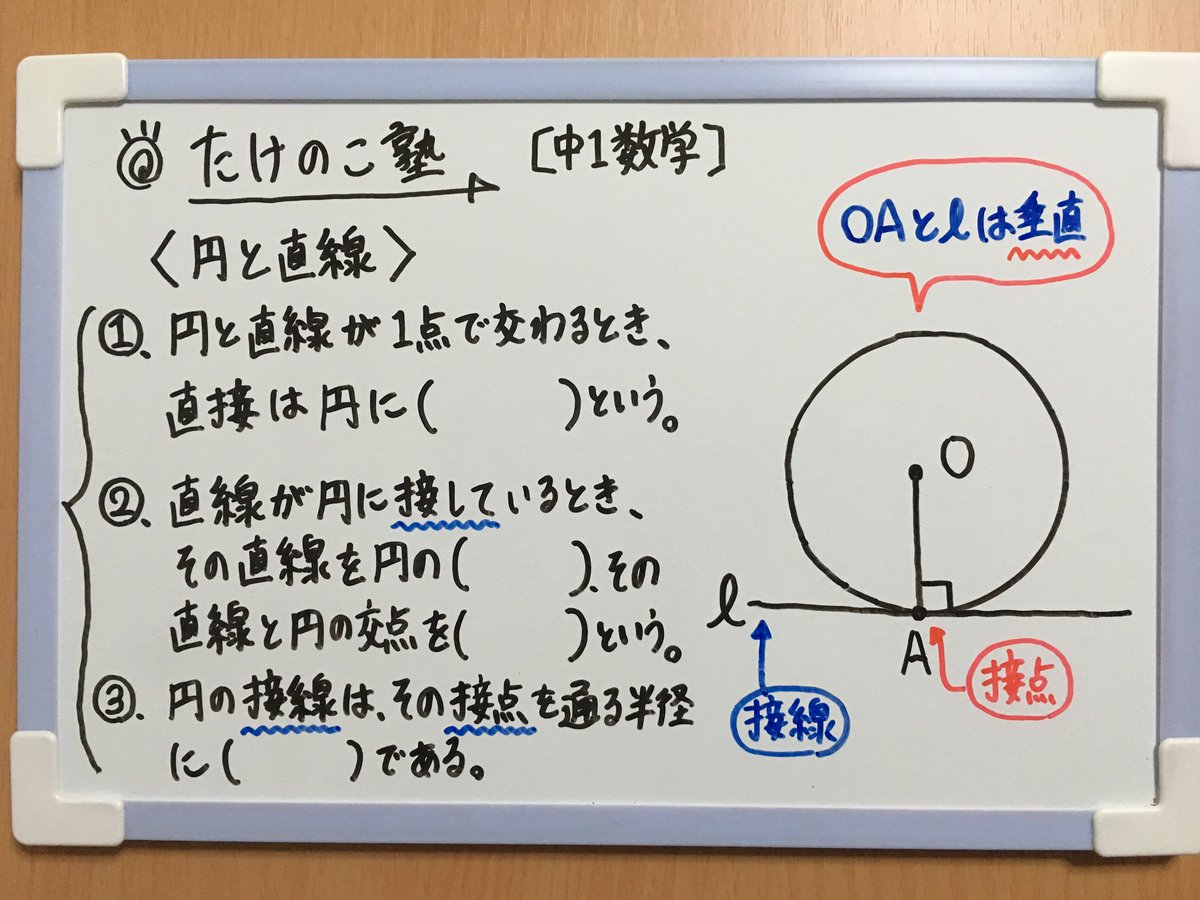



たけのこ塾 中1数学 今回は 円と直線 についての問題です 円と直線が1点で交わるとき 直線は円に接するという のとき 直線を円の接線 直線と円の交点を接点という 円の接線は その接点を通る半径に垂直である 勉強垢 中1 数学



2つの円の円弧接線を描く Rhinocerosの使い方




002 円と直線が接するときの接点の座標 Youtube



0 件のコメント:
コメントを投稿